zkMe zkVault

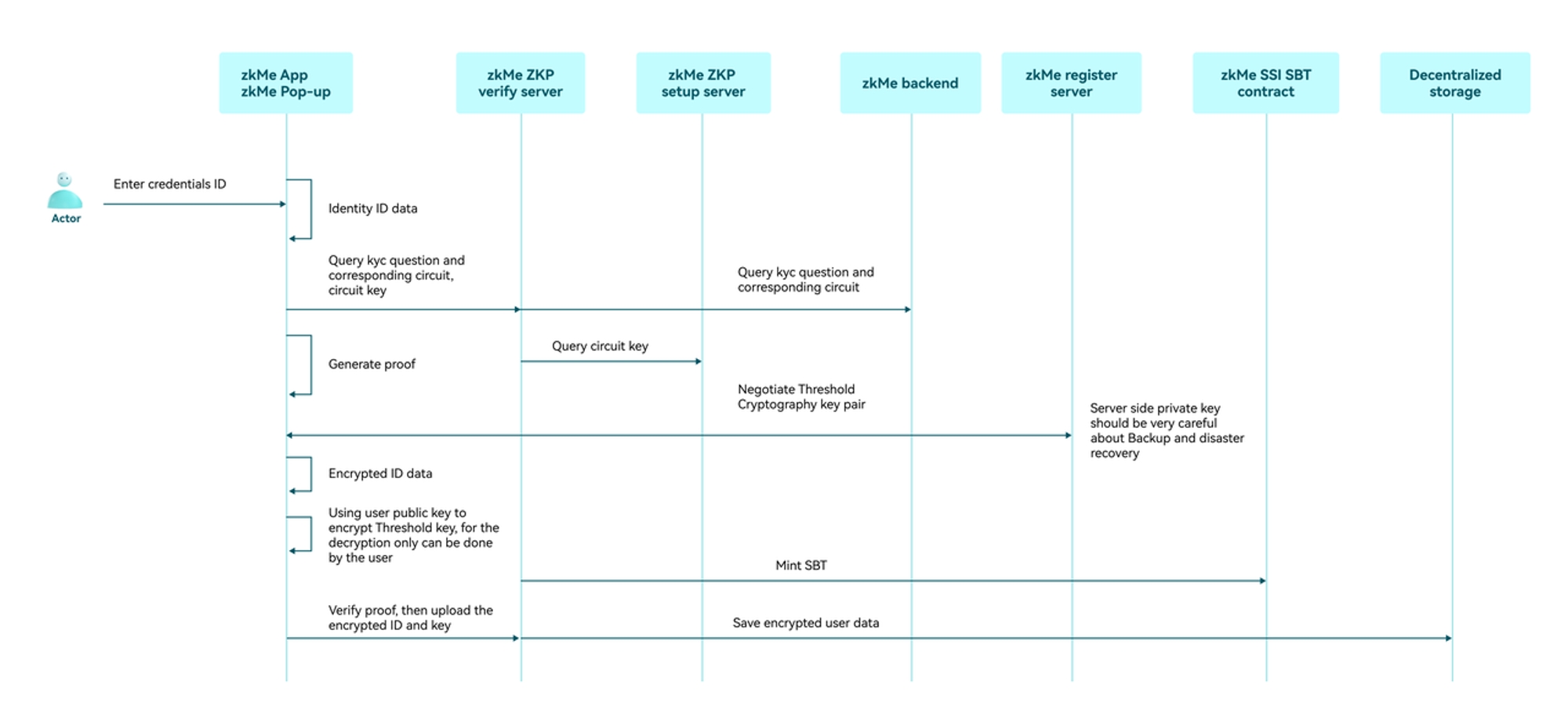
This section explains the zkMe data recovery procedure enabled by the zkMe Data Vault required to fulfill KYC data storage and retention requirements in major regulatory jurisdictions.

Vault Overview

The use of decentralized storage combined with threshold ensures that only authorized parties can access these documents under strict predetermined conditions and strict collaboration between all involved stakeholders. At no point in time is a single stakeholder able to unlock the private data of the Holder. In threshold encryption, a group of n participants collaboratively generate a public key, while the decryption key is shared among them. The Holder stays anonymous until proven guilty.

The public key can be used to encrypt messages directly, but decryption requires the participation of a minimum number of t participants among the n participants to obtain the correct plaintext. A crypto system that requires at least t participants to decrypt is called a (t/n) threshold crypto system.

Encryption/ decryption process

The public key can be used to encrypt messages directly, but decryption requires the participation of a minimum number of t participants among the n participants to obtain the correct plaintext. A crypto system that requires at least t participants to decrypt is called a (t/n) threshold crypto system.

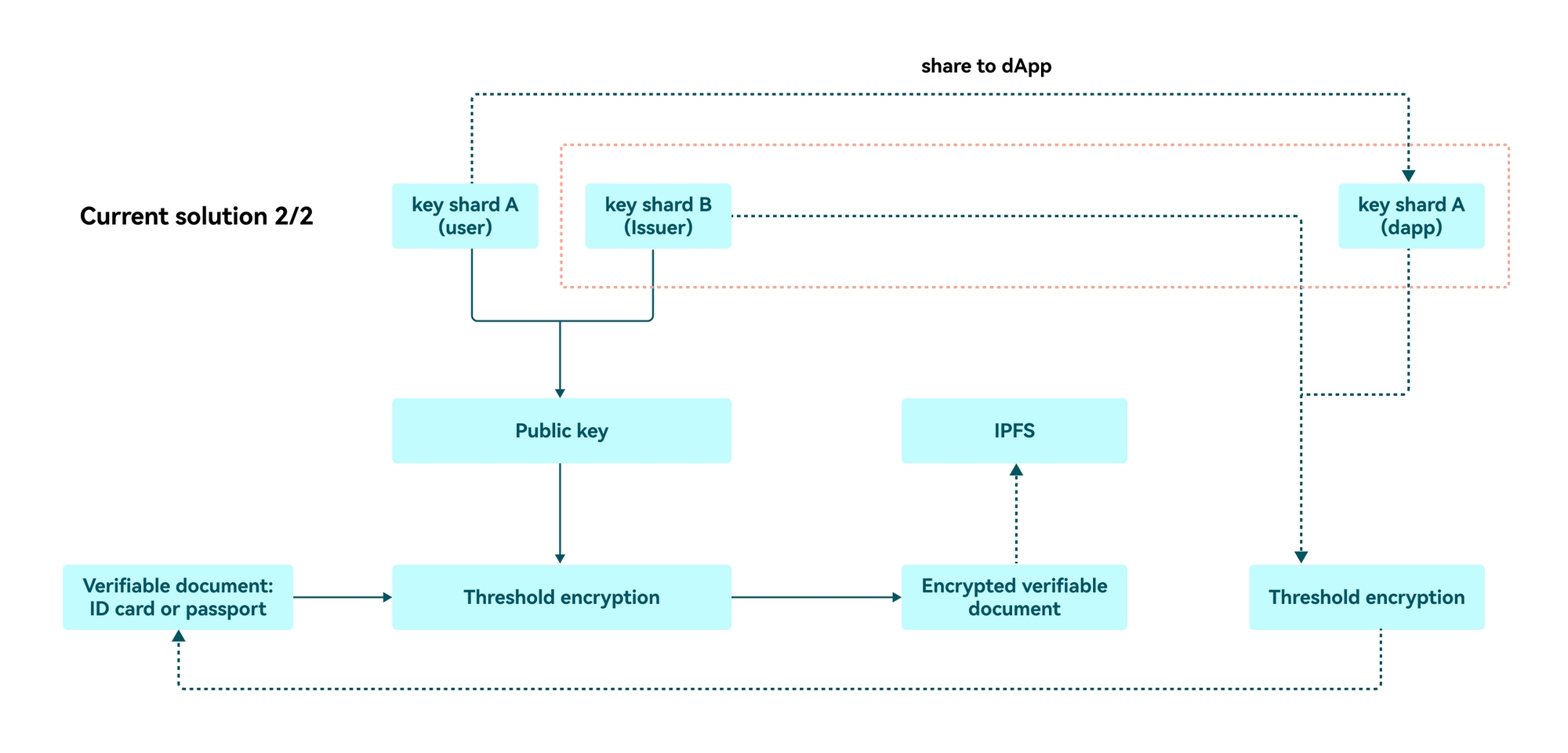
The zkMe protocol implements a (2/2) threshold cryptosystem (to be expanded to 3/3 in future iterations, see below).

Here, two-party EC-ElGamal scheme: Two-party computation of ciphertexts, the global decryption key is given by: $x = x_1 + x_2 \ mod p$ , in additive key share form. The global encryption key is given by ℎ = 𝑥 ∗ 𝑃:

Notation

Symbol	Notion	Symbol	Notion
$P$	Elliptic curve base point	$x$	Global private key(no one knows it)(type: scalar)
$p$	Order of the base point	$h$	Global public key(type: ecpoint)
$\mathbf{𝑍_𝑛}$	Field of operations for elliptic curves	$x_i$	party-i 's private key (key share of )(type: scalar)
+	Addition operation in numerical terms	$h_i$	Point addition operation on elliptic curves
*	Multiplication operation in numerical terms	$\mathbf{𝑐_𝑖}$	party-i 's commitment(type: scalar)
$\mathbf{⊕}$	Point addition operation on elliptic curves	$\mathbf{𝑟_𝑖}$	Random number(type: scalar)
$\mathbf{⊗}$	Point doubling operation on elliptic curves	$m$	message
$𝐻$	keccak256	ciphertext	ciphertext of m under AES with symmetric key
𝑘𝑝𝑜𝑖𝑛𝑡	Point can derive the symmetric key	sym_key	sym_key k

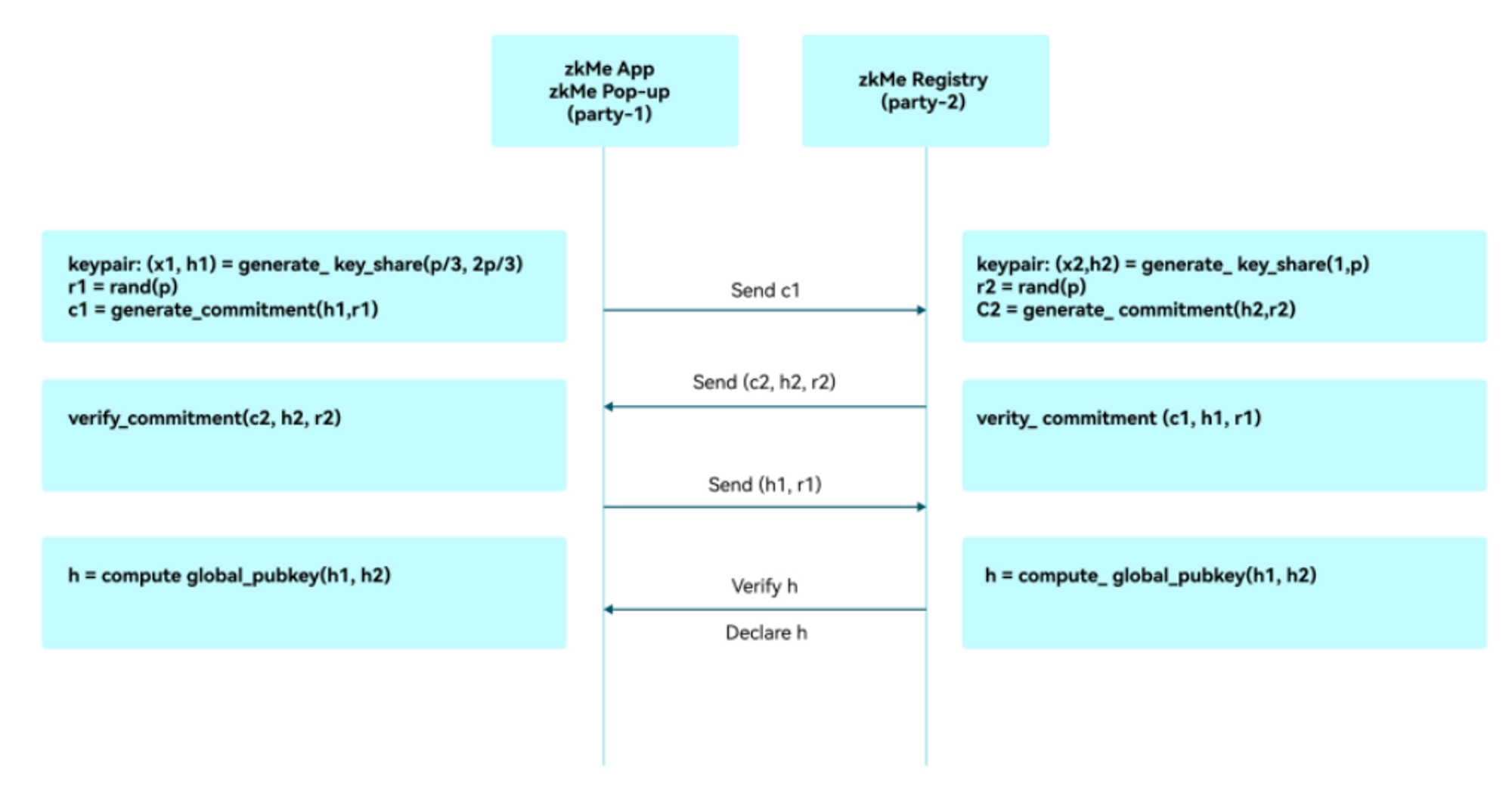
Phase 1: Global public key negotiation

The threshold encryption public key negotiation goes through the following steps.

1. Generate the keypair $(𝑥_1 ,ℎ_1)$ for party-1 regarding ℎ and make a commitment $𝑐_1= 𝐻(ℎ_1 ,𝑟_1)$ for $ℎ_1$. Generate keypair $(𝑥_2 ,ℎ_2)$ for party-2 regarding ℎ and make a commitment $𝑐_2=𝐻(ℎ_2 ,𝑟_2)$ for $ℎ_2$.

Function	Operation
generate_key_share(m, n) at party-i	𝑥𝑖 ⟵𝑅 [𝑚,𝑛], ℎ𝑖=𝑥𝑖⊗𝑃
rand(p) at party-i	𝑟 ⟵𝑅 [1,𝑝]
generate_commitment(m, n) at party-i	𝑐=𝐻(𝑚 ||𝑛)
verify_commitment(c, m, n) at party-i	𝑐′=𝐻(𝑚 ||𝑛), check 𝑐== 𝑐′

2. Party-1 sends $𝑐_1$ to party-2.
3. Party-2 sends $𝑐_2$ and the preimage ($ℎ_2 ,𝑟_2$) of $𝑐_2$ to party-1.
4. Party-1 verifies $𝑐_2=𝐻(ℎ_2 ,𝑟_2)$ and then sends the preimage ($ℎ_1 , 𝑟_1$) of $𝑐_1$ to party-2.
5. Party-2 verifies $𝑐_1=𝐻(ℎ_1 ,𝑟_1)$ .
6. Party-1 and party-2 each compute $ℎ=ℎ_1+ℎ_2$, confirm that the results are the same, and jointly announce the global encryption key as $ℎ$.

Function	Operation
compute_global_pubkey(m,n) at party-i	ℎ=𝑚⊕𝑛

Phase 2: Encryption

The following process is standard hybrid encryption using EC-ElGamal, assuming that the encryption party has already obtained the global encryption key ℎ through the following steps:

1. The encrypting party calls generate_sym_key(p) to generate a random 𝑘𝑝𝑜𝑖𝑛𝑡, and then calls compute_sym_key($𝑘_{𝑝𝑜𝑖𝑛𝑡}$) to compute the symmetric key pair sym_key.

Function	Operation
generate_key_point(p) at party-i	𝑘 ⟵𝑅 [1,𝑝], $𝑘_{𝑝𝑜𝑖𝑛𝑡}$=𝑘⊗𝑃
compute_sym_key( 𝑘𝑝𝑜𝑖𝑛𝑡) at party-i	𝑠𝑦𝑚_𝑘𝑒𝑦=𝐻(𝑝𝑜𝑖𝑛𝑡2𝑏𝑦𝑡𝑒𝑠($𝑘_{𝑝𝑜𝑖𝑛𝑡}$))

2. The encrypting party calls the AES algorithm to encrypt the message m using the symmetric key sym_key to obtain the symmetric ciphertext 𝑒𝑛𝑐, and then uses EC-ElGamal to encrypt by calling elgamal_encrypt($𝑘_{𝑝𝑜𝑖𝑛𝑡}, ℎ$) to obtain ( 𝐶1,𝐶2 ).

Function	Operation
elgamal_encrypt( $𝑘_{𝑝𝑜𝑖𝑛𝑡}, h$) at encrypt-party	𝑟 ⟵𝑅 [1,𝑝], 𝐶1=𝑟⊗𝑃, 𝐶2=$𝑘_{𝑝𝑜𝑖𝑛𝑡}$⊕ (𝑟⊗ℎ)

3. The ciphertext (ciphertext, 𝐶1,𝐶2 ) is made public.

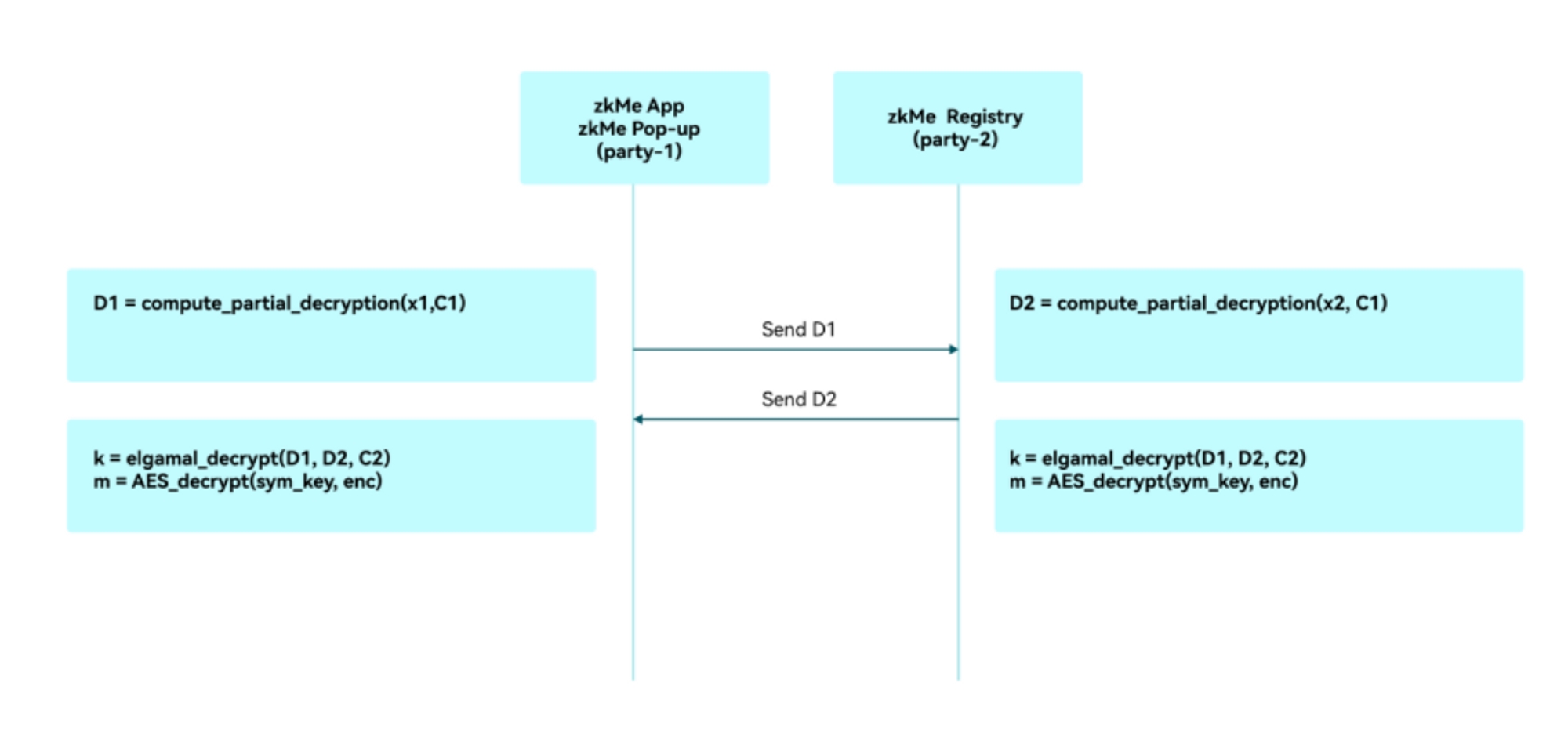
Phase 3: Threshold decryption

In case regulators initiate bad actor proceedings, the threshold cryptography protecting the raw data of the user can be recovered using the following steps:

1. Each party-i calculates the partial decryption $𝐷_𝑖$ with respect to $𝐶_1$.

Function	Operation
compute_partial_decryption($xi$, $C_1$) at party-i	𝐷𝑖 =𝑥𝑖⊗ $𝐶_1$

2. Party-i sends $𝐷_𝑖$ to party-3-i.
3. Party-i locally calls elgamal_decrypt(D1, D2, C2) to obtain , and then calls compute_sym_key($𝑘_{𝑝𝑜𝑖𝑛𝑡}$) to compute the symmetric key pair sym_key.

Function	Operation
elgamal_decrypt(D1, D2, C2) at party-i	𝐷= 𝐷1⊕𝐷2, $𝑘_{𝑝𝑜𝑖𝑛𝑡}$ = 𝐶2 ⊕ (−𝐷)

4. Party-i calls the AES algorithm to decrypt the symmetric ciphertext 𝑒𝑛𝑐 using the symmetric key sym_key to obtain the message m

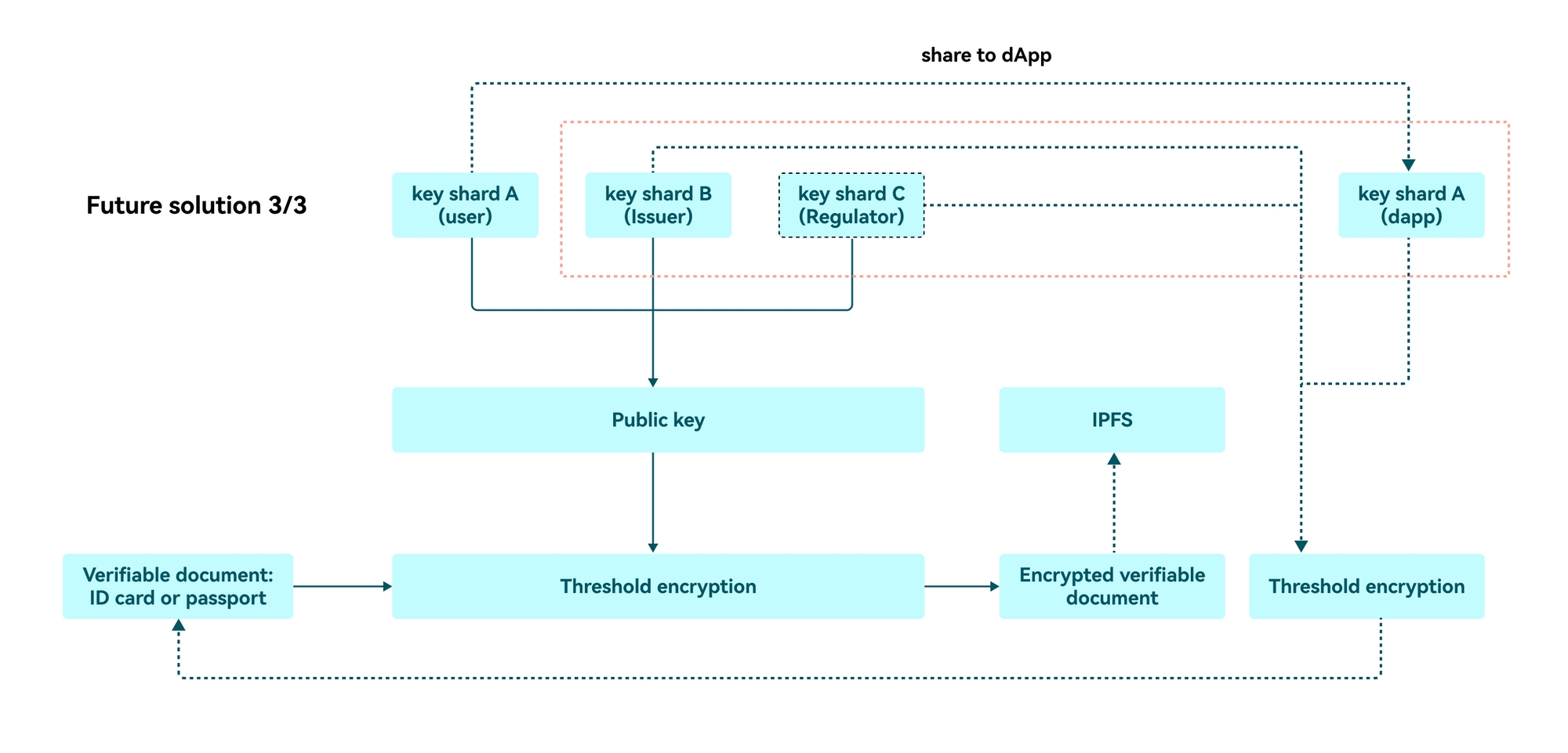
Future extension: (3/3) threshold

As shown in the figure below, the (3/3) threshold cryptosystem will be implemented in the next phase. zkMe is currently communicating with different jurisdictions to improve the entire procedure.

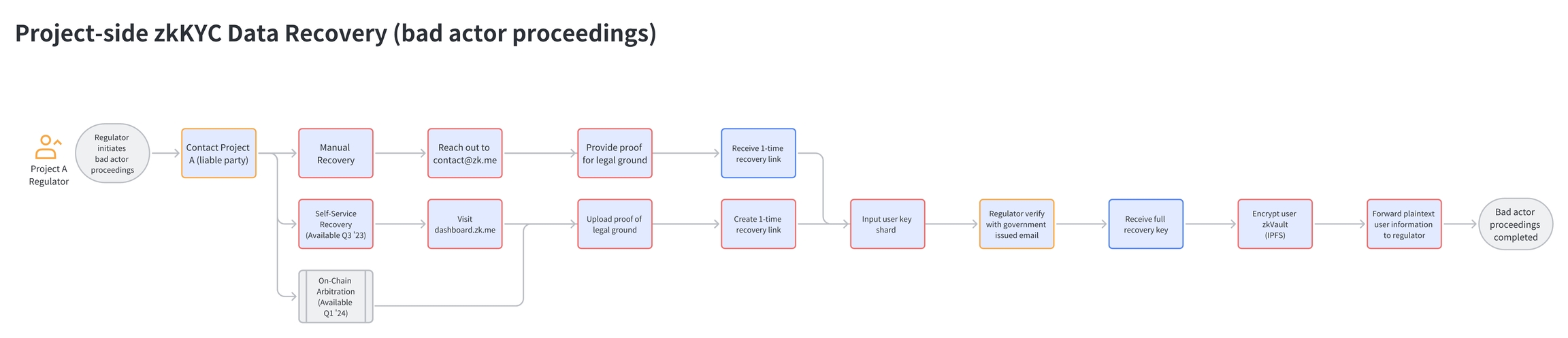
Retrieval Procedure

1. Preliminary Investigation: Law enforcement conducts a preliminary investigation to gather evidence and establish reasonable suspicion or probable cause related to the user's activities.

2. Legal Process: Law enforcement obtains the necessary legal authorization, such as a warrant or court order, to access the user's identity document.

3. Contact Verifier Governance: Law enforcement reaches out to the web3 protocol governance with the user's digital asset wallet address and provides the legal authorization obtained in step 2.

4. Verify Legal Request: The web3 protocol governance verifies the legitimacy of the legal request and confirms the scope of the information required.

5. Stakeholder Collaboration: Each stakeholder (issuer, verifier, regulator) verifies the legal request independently. If they determine that the request is valid, they agree to participate in the decryption process.

6. Threshold Decryption: The stakeholders collaboratively decrypt the user's Identity document using their respective decryption key shares. This process ensures that no single stakeholder can access the private data of the user without the required collaboration.

7. Provide Decrypted Document: Once the user's Identity document has been decrypted, the web3 Protocol Governance provides the decrypted document to law enforcement within the scope of the legal authorization.

---

Exkursus: KYC Data Storage and Retention Requirements in Major Jurisdictions

The Know Your Customer (KYC) process is an essential part of financial institutions' efforts to combat money laundering, terrorist financing, and other illicit activities. Regulatory authorities around the world have established guidelines for KYC data storage and retention to ensure the availability of information for investigations and to maintain the integrity of the financial system. Below are the requirements in some major jurisdictions:

United States

In the United States, the Bank Secrecy Act (BSA) and the USA PATRIOT Act outline the requirements for financial institutions regarding KYC data storage and retention. According to these regulations, financial institutions are required to:

• Retain records of customer identification information for five years after the account is closed or the relationship is terminated.

• Keep records of suspicious activity reports (SARs) and currency transaction reports (CTRs) for at least five years.

European Union

In the European Union, the Anti-Money Laundering Directive (AMLD) governs the KYC data storage and retention requirements for financial institutions. Under the AMLD, financial institutions are required to:

• Retain customer due diligence (CDD) records and supporting documentation for at least five years after the end of the business relationship or the completion of an occasional transaction.

• Delete personal data after the retention period, unless national law requires a longer storage period for specific purposes.

United Kingdom

In the United Kingdom, the Money Laundering Regulations (MLRs) outline the KYC data storage and retention requirements. Under the MLRs, financial institutions are required to:

• Retain records of CDD measures and transactions for at least five years after the end of the business relationship or the completion of an occasional transaction.

• Delete personal data after the retention period, unless there are legal or regulatory reasons to retain it for a longer period.

China

In China, the Anti-Money Laundering Law (AMLL) and the People's Bank of China (PBOC) regulations govern the KYC data storage and retention requirements for financial institutions. According to these regulations, financial institutions are required to:

• Retain records of customer identification information and transaction records for at least five years from the date the transaction or account activity occurred.

• Keep records of large-value and suspicious transactions for at least five years.

Hong Kong

In Hong Kong, the Anti-Money Laundering and Counter-Terrorist Financing Ordinance (AMLO) and guidelines issued by the Hong Kong Monetary Authority (HKMA) govern the KYC data storage and retention requirements for financial institutions. According to these regulations, financial institutions are required to:

• Retain records of customer identification information and transaction records for at least six years after the end of the business relationship or the completion of an occasional transaction.

• Keep records of suspicious transaction reports (STRs) for at least six years.

Singapore

In Singapore, the Monetary Authority of Singapore (MAS) enforces the Anti-Money Laundering and Countering the Financing of Terrorism (AML/CFT) rules, which outline the KYC data storage and retention requirements for financial institutions. Under these rules, financial institutions are required to:

• Retain records of customer due diligence (CDD) measures, including customer identification information, account files, and business correspondence, for at least five years after the end of the business relationship or the completion of an occasional transaction.

• Keep records of transaction records and STRs for at least five years from the date of the transaction or the submission of the STR.

Reference

Financial Crimes Enforcement Network. (n.d.). Bank Secrecy Act regulations. Retrieved from https://www.fincen.gov/resources/statutes-regulations/bsa-regulations

U.S. Department of the Treasury. (n.d.). USA PATRIOT Act. Retrieved from https://home.treasury.gov/policy-issues/office-of-terrorism-and-financial-intelligence/usa-patriot-act

European Parliament and Council of the European Union. (2018). Directive (EU) 2018/843. Retrieved from https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32018L0843

HM Government. (2017). The Money Laundering, Terrorist Financing and Transfer of Funds (Information on the Payer) Regulations 2017. Retrieved from https://www.legislation.gov.uk/uksi/2017/692/contents/made

National People's Congress. (2006). Anti-Money Laundering Law of the People's Republic of China. Retrieved from http://www.npc.gov.cn/englishnpc/Law/2009-02/20/content_1471587.htm

People's Bank of China. (n.d.). People's Bank of China regulations. Retrieved from http://www.pbc.gov.cn/en/3688016/index.html

Hong Kong Government. (2012). Anti-Money Laundering and Counter-Terrorist Financing Ordinance. Retrieved from https://www.elegislation.gov.hk/hk/cap615

Hong Kong Monetary Authority. (n.d.). Guidelines on Anti-Money Laundering and Counter-Financing of Terrorism. Retrieved from https://www.hkma.gov.hk/eng/regulatory-resources/anti-money-laundering-and-counter-financing-of-terrorism/guidelines/

Monetary Authority of Singapore. (n.d.). Anti-Money Laundering and Countering the Financing of Terrorism. Retrieved from https://www.mas.gov.sg/regulation/anti-money-laundering